Analyzing the Graph of Thrones
William Lyon / June 26, 2016
14 min read •
A few months ago, mathematicians Andrew Beveridge and Jie Shan published Network of Thrones in Math Horizon Magazine where they analyzed a network of character interactions from the novel "A Storm of Swords", the third book in the popular "A Song of Ice and Fire" and the basis for the Game of Thrones TV series. In their paper they detail how they constructed the network of character interactions by using text analysis and entity extraction to find characters mentioned together in the text. They then applied social network analysis algorithms to the network to find the most important characters in the network and a community detection algorithm to find clusters of characters.
The analysis and visualization was done using Gephi, a popular graph analytics tool. I thought it would be fun to try to duplicate the authors' results using Neo4j.
Import initial data into Neo4j
The data was made available on the authors' website which you can download here. It looks like this:
Source,Target,Weight
Aemon,Grenn,5
Aemon,Samwell,31
Aerys,Jaime,18
...
Here we have an adjacency list of characters and their number of interactions throughout the text. We will use a simple data model (:Character {name})-[:INTERACTS {weight}]->(:Character {name}). Nodes with the label Character to represent characters from the text, with a single relationship type INTERACTS connecting characters who have interacted in the text. We'll store the character's name as property name on the node and the number of interactions between two characters as a property weight on the relationships.
We first must create a constraint to assert the integrity of our schema:
CREATE CONSTRAINT ON (c:Character) ASSERT c.name IS UNIQUE;
Once the constraint is created (this statement will also build an index which will improve the performance of lookups by character name) we can use the Cypher LOAD CSV statement to import the data:
LOAD CSV WITH HEADERS FROM "https://www.macalester.edu/~abeverid/data/stormofswords.csv" AS row
MERGE (src:Character {name: row.Source})
MERGE (tgt:Character {name: row.Target})
MERGE (src)-[r:INTERACTS]->(tgt)
ON CREATE SET r.weight = toInt(row.Weight)
We have a very simple datamodel:
CALL apoc.meta.graph()
The graph of thrones datamodel. Character nodes are connected by an INTERACTS relationship.
We can visualize the entire graph, but this doesn't give us much information about the most important characters or how they interact:
MATCH p=(:Character)-[:INTERACTS]-(:Character)
RETURN p
Analyzing the network
We'll use Cypher, the graph query language to explore the graph of thrones, applying some tools from network analysis along the way. Many of the ideas explored here are explained in detail in the excellent Networks, Crowds, and Markets: Reasoning About a Highly Connected World.
Number of characters#
Let's start with something simple. How many characters appear in our graph?
MATCH (c:Character) RETURN count(c)
╒════════╕
│count(c)│
╞════════╡
│107 │
└────────┘
Summary statistics#
Summary statistics for number of other characters each character has interacted with:
MATCH (c:Character)-[:INTERACTS]->()
WITH c, count(*) AS num
RETURN min(num) AS min, max(num) AS max, avg(num) AS avg_characters, stdev(num) AS stdev
╒═══╤═══╤═════════════════╤═════════════════╕
│min│max│avg_characters │stdev │
╞═══╪═══╪═════════════════╪═════════════════╡
│1 │24 │4.957746478873241│6.227672391875085│
└───┴───┴─────────────────┴─────────────────┘
Diameter of the network#
The diameter (or geodesic) of a network is defined as the longest shortest path in the network.
// Find maximum diameter of network
// maximum shortest path between two nodes
MATCH (a:Character), (b:Character) WHERE id(a) > id(b)
MATCH p=shortestPath((a)-[:INTERACTS*]-(b))
RETURN length(p) AS len, extract(x IN nodes(p) | x.name) AS path
ORDER BY len DESC LIMIT 4
╒═══╤════════════════════════════════════════════════════════════╕
│len│path │
╞═══╪════════════════════════════════════════════════════════════╡
│6 │[Illyrio, Belwas, Daenerys, Robert, Tywin, Oberyn, Amory] │
├───┼────────────────────────────────────────────────────────────┤
│6 │[Illyrio, Belwas, Daenerys, Robert, Sansa, Bran, Jojen] │
├───┼────────────────────────────────────────────────────────────┤
│6 │[Illyrio, Belwas, Daenerys, Robert, Stannis, Davos, Shireen]│
├───┼────────────────────────────────────────────────────────────┤
│6 │[Illyrio, Belwas, Daenerys, Robert, Sansa, Bran, Luwin] │
└───┴────────────────────────────────────────────────────────────┘
We can see there are many paths of length six in the network.
Shortest path#
We can use the shortestPath function in Cypher to find the shortest path between any two characters in the graph. Let's find the shortest path from Catelyn Stark to Kahl Drogo:
// Shortest path from Catelyn Stark to Khal Drogo
MATCH (catelyn:Character {name: "Catelyn"}), (drogo:Character {name: "Drogo"})
MATCH p=shortestPath((catelyn)-[INTERACTS*]-(drogo))
RETURN p
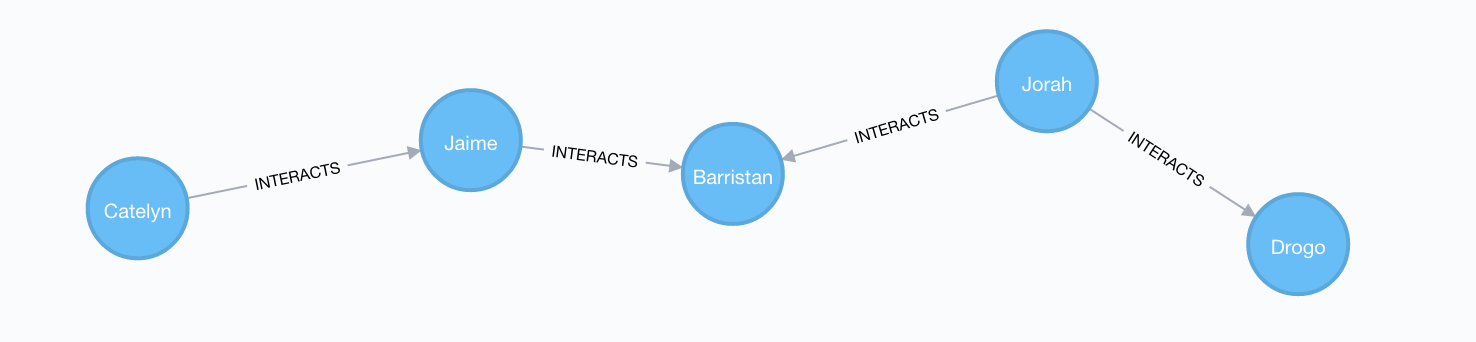
All Shortest Paths#
There might be other paths of the same length connecting Catelyn and Drogo. We can find these with the allShortestPaths Cypher function:
// All shortest paths from Catelyn Stark to Khal Drogo
MATCH (catelyn:Character {name: "Catelyn"}), (drogo:Character {name: "Drogo"})
MATCH p=allShortestPaths((catelyn)-[INTERACTS*]-(drogo))
RETURN p
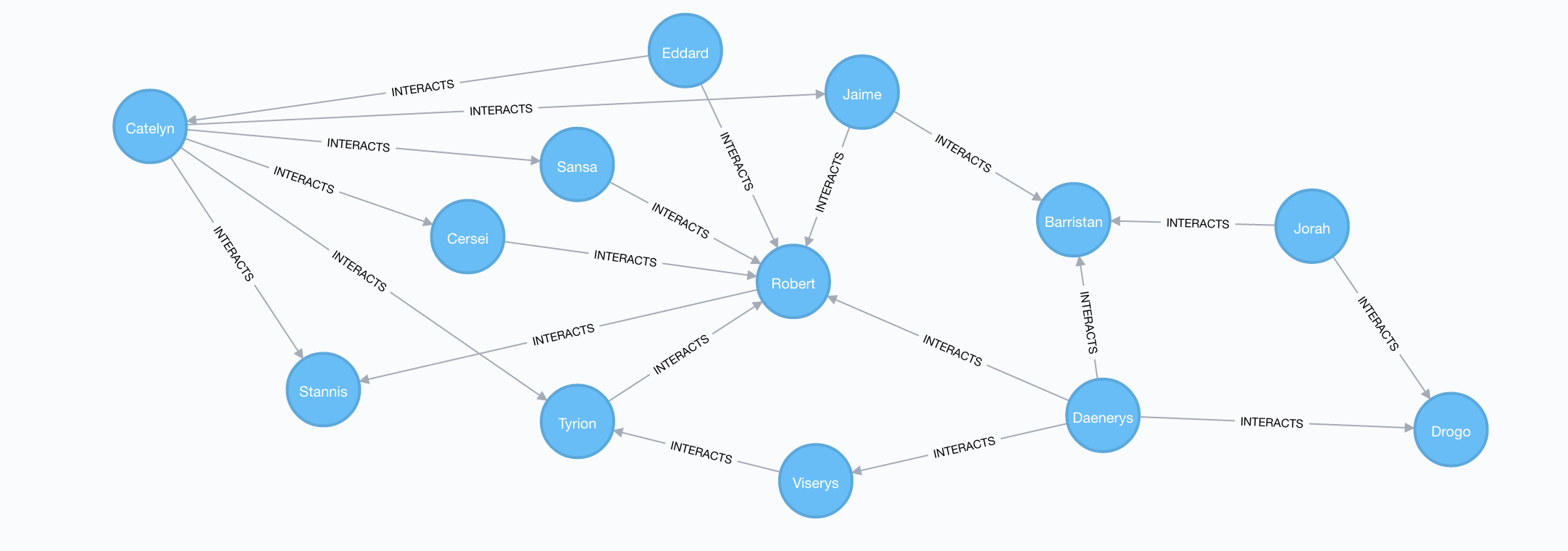
Pivotal nodes
A node is said to be pivotal if it lies on all shortest paths between two other nodes in the network. We can find all pivotal nodes in the network:
// Find all pivotal nodes in network
MATCH (a:Character), (b:Character)
MATCH p=allShortestPaths((a)-[:INTERACTS*]-(b)) WITH collect(p) AS paths, a, b
MATCH (c:Character) WHERE all(x IN paths WHERE c IN nodes(x)) AND NOT c IN [a,b]
RETURN a.name, b.name, c.name AS PivotalNode SKIP 490 LIMIT 10
╒═══════╤═══════╤═══════════╕
│a.name │b.name │PivotalNode│
╞═══════╪═══════╪═══════════╡
│Aegon │Thoros │Daenerys │
├───────┼───────┼───────────┤
│Aegon │Thoros │Robert │
├───────┼───────┼───────────┤
│Drogo │Ramsay │Robb │
├───────┼───────┼───────────┤
│Styr │Daario │Daenerys │
├───────┼───────┼───────────┤
│Styr │Daario │Jon │
├───────┼───────┼───────────┤
│Styr │Daario │Robert │
├───────┼───────┼───────────┤
│Qhorin │Podrick│Jon │
├───────┼───────┼───────────┤
│Qhorin │Podrick│Sansa │
├───────┼───────┼───────────┤
│Orell │Theon │Jon │
├───────┼───────┼───────────┤
│Illyrio│Bronn │Belwas │
└───────┴───────┴───────────┘
If we look through the result table for interesting results we can see that Robb is a pivotal node for Drogo and Ramsay. This means that all shortest paths connecting Drogo and Ramsay pass through Robb. We can verify this visually by looking at all shortest paths connecting Drogo and Ramsay:
MATCH (a:Character {name: "Drogo"}), (b:Character {name: "Ramsay"})
MATCH p=allShortestPaths((a)-[:INTERACTS*]-(b))
RETURN p
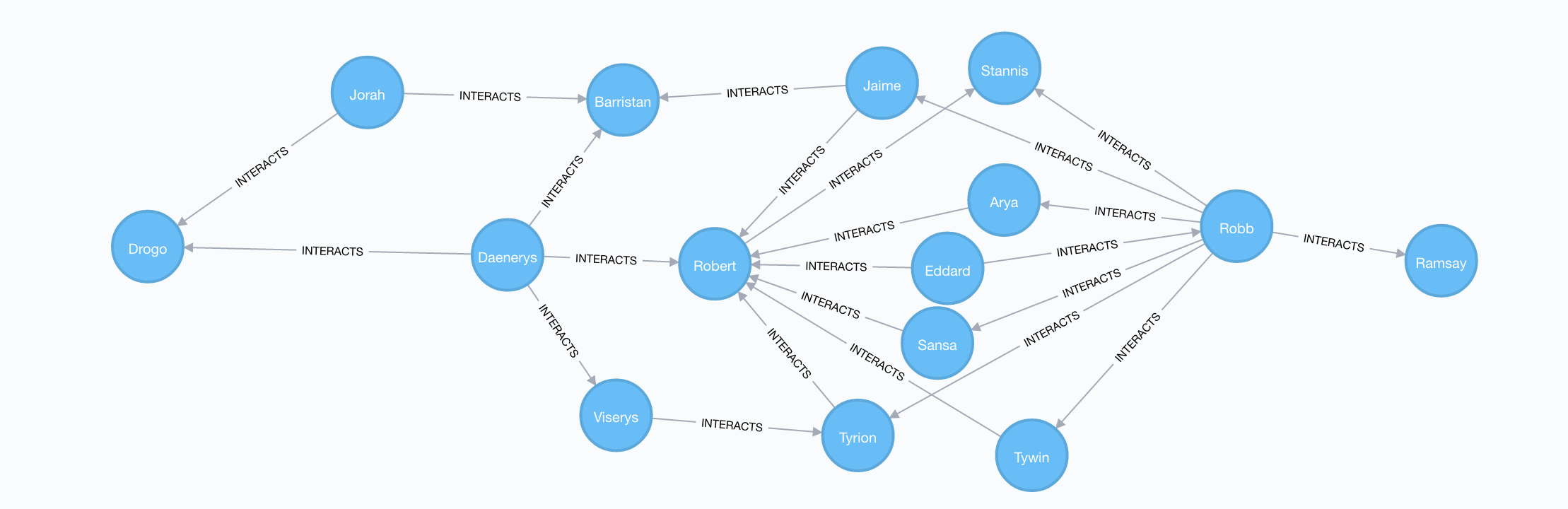
Centrality measures
Centrality measures give us relative measures of importance in the network. There are many different centrality measures and each measures a different type of "importance".
Degree Centrality#
Degree centrality is simply the number of connections that a node has in the the network. In the context of the graph of thrones, the degree centrality of a character is the number of other characters that character interacted with. We can calculate degree centrality using Cypher like this:
MATCH (c:Character)
RETURN c.name AS character, size( (c)-[:INTERACTS]-() ) AS degree ORDER BY degree DESC
╒═════════╤══════╕
│character│degree│
╞═════════╪══════╡
│Tyrion │36 │
├─────────┼──────┤
│Jon │26 │
├─────────┼──────┤
│Sansa │26 │
├─────────┼──────┤
│Robb │25 │
├─────────┼──────┤
│Jaime │24 │
├─────────┼──────┤
│Tywin │22 │
├─────────┼──────┤
│Cersei │20 │
├─────────┼──────┤
│Arya │19 │
├─────────┼──────┤
│Joffrey │18 │
├─────────┼──────┤
│Robert │18 │
└─────────┴──────┘
And we see that Tyrion has interacted with the most characters in the network. Given his scheming, I think this makes sense.
Weighted Degree Centrality#
We are storing the number of interactions between a pair of characters as a property weight on the INTERACTS relationship. Summing this weight across all INTERACTS relationships for the character gives us their weighted degree centrality, or the total number of interactions in which they participated. Again, we can use Cypher to calculate this metric for all characters:
MATCH (c:Character)-[r:INTERACTS]-()
RETURN c.name AS character, sum(r.weight) AS weightedDegree ORDER BY weightedDegree DESC
╒═════════╤══════════════╕
│character│weightedDegree│
╞═════════╪══════════════╡
│Tyrion │551 │
├─────────┼──────────────┤
│Jon │442 │
├─────────┼──────────────┤
│Sansa │383 │
├─────────┼──────────────┤
│Jaime │372 │
├─────────┼──────────────┤
│Bran │344 │
├─────────┼──────────────┤
│Robb │342 │
├─────────┼──────────────┤
│Samwell │282 │
├─────────┼──────────────┤
│Arya │269 │
├─────────┼──────────────┤
│Joffrey │255 │
├─────────┼──────────────┤
│Daenerys │232 │
└─────────┴──────────────┘
Betweenness Centrality#
The betweenness centrality of a node in a network is the number of shortest paths between two other members in the network on which a given node appears. Betweenness centality is an important metric because it can be used to identify "brokers of information" in the network or nodes that connect disparate clusters.
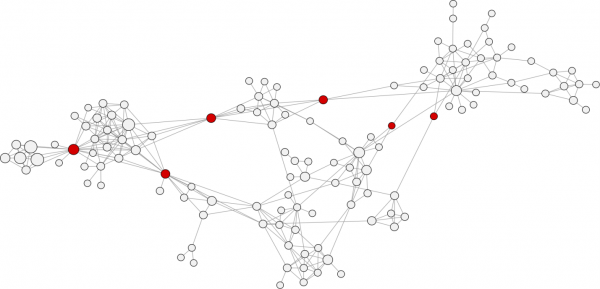The red nodes have a high betweenness centrality and are connectors of clusters. Image credit
To calculate betweenness centrality we will use the new Awesome Procedures for Neo4j 3.x or apoc library. Once we've installed apoc we can call any of the 170+ procedures from Cypher:
MATCH (c:Character)
WITH collect(c) AS characters
CALL apoc.algo.betweenness(['INTERACTS'], characters, 'BOTH') YIELD node, score
SET node.betweenness = score
RETURN node.name AS name, score ORDER BY score DESC
╒════════╤══════════════════╕
│name │score │
╞════════╪══════════════════╡
│Jon │1279.7533534055322│
├────────┼──────────────────┤
│Robert │1165.6025171231624│
├────────┼──────────────────┤
│Tyrion │1101.3849724234349│
├────────┼──────────────────┤
│Daenerys│874.8372110508583 │
├────────┼──────────────────┤
│Robb │706.5572832464792 │
├────────┼──────────────────┤
│Sansa │705.1985623519137 │
├────────┼──────────────────┤
│Stannis │571.5247305125714 │
├────────┼──────────────────┤
│Jaime │556.1852522889822 │
├────────┼──────────────────┤
│Arya │443.01358430043337│
├────────┼──────────────────┤
│Tywin │364.7212195528086 │
└────────┴──────────────────┘
Closeness centrality#
Closeness centrality is the inverse of the average distance to all other characters in the network. Nodes with high closeness centality are often highly connected within clusters in the graph, but not necessarily highly connected outside of the cluster.
Nodes with high closeness centrality are connected to many other nodes in a network. Image credit
MATCH (c:Character)
WITH collect(c) AS characters
CALL apoc.algo.closeness(['INTERACTS'], characters, 'BOTH') YIELD node, score
RETURN node.name AS name, score ORDER BY score DESC
╒═══════╤═════════════════════╕
│name │score │
╞═══════╪═════════════════════╡
│Tyrion │0.004830917874396135 │
├───────┼─────────────────────┤
│Sansa │0.004807692307692308 │
├───────┼─────────────────────┤
│Robert │0.0047169811320754715│
├───────┼─────────────────────┤
│Robb │0.004608294930875576 │
├───────┼─────────────────────┤
│Arya │0.0045871559633027525│
├───────┼─────────────────────┤
│Jaime │0.004524886877828055 │
├───────┼─────────────────────┤
│Stannis│0.004524886877828055 │
├───────┼─────────────────────┤
│Jon │0.004524886877828055 │
├───────┼─────────────────────┤
│Tywin │0.004424778761061947 │
├───────┼─────────────────────┤
│Eddard │0.004347826086956522 │
└───────┴─────────────────────┘
Using python-igraph
One of the things I love about Neo4j is how well it works with other tools, things like R and Python data science tools. We could continue to use apoc to run PageRank and community detection algorithms, but let's switch to using python-igraph to calculate some analyses. Python-igraph is a port of the R igraph graph analytics library. To install, just use pip install python-igraph.
Building an igraph instance from Neo4j#
To use igraph on our graph of thrones data, the first thing we need to do is pull data out of Neo4j and build an igraph instnace in Python. We can do this using py2neo, one of the Python drivers for Neo4j. We can pass the results object of a Py2neo query directly into the TupleList constructor of igraph to create an igraph instance:
from py2neo import Graph
from igraph import Graph as IGraph
graph = Graph()
query = '''
MATCH (c1:Character)-[r:INTERACTS]->(c2:Character)
RETURN c1.name, c2.name, r.weight AS weight
'''
ig = IGraph.TupleList(graph.run(query), weights=True)
We now have an igraph object that we can use to run any of the graph algorithms implemented in igraph.
PageRank#
The first algorithm we'll use in igraph is PageRank. PageRank is an algorithm originally used by Google to rank the importance of web pages and is a type of eigenvector centrality.
PageRank: The size of each node is proportional to the number and size of the other nodes pointing to it in the network. Image credit wikipedia CC-BY
Here's we'll run Pagerank on our igraph instance, then write the results back to Neo4j, creating a pagerank property on our Character nodes to store the value we just calculated in igraph:
pg = ig.pagerank()
pgvs = []
for p in zip(ig.vs, pg):
print(p)
pgvs.append({"name": p[0]["name"], "pg": p[1]})
pgvs
write_clusters_query = '''
UNWIND {nodes} AS n
MATCH (c:Character) WHERE c.name = n.name
SET c.pagerank = n.pg
'''
graph.run(write_clusters_query, nodes=pgvs)
We can now query our graph in Neo4j to find the nodes with the highest PageRank score:
MATCH (n:Character)
RETURN n.name AS name, n.pagerank AS pagerank ORDER BY pagerank DESC LIMIT 10
╒════════╤════════════════════╕
│name │pagerank │
╞════════╪════════════════════╡
│Tyrion │0.042884981999963316│
├────────┼────────────────────┤
│Jon │0.03582869669163558 │
├────────┼────────────────────┤
│Robb │0.03017114665594764 │
├────────┼────────────────────┤
│Sansa │0.030009716660108578│
├────────┼────────────────────┤
│Daenerys│0.02881425425830273 │
├────────┼────────────────────┤
│Jaime │0.028727587587471206│
├────────┼────────────────────┤
│Tywin │0.02570016262642541 │
├────────┼────────────────────┤
│Robert │0.022292016521362864│
├────────┼────────────────────┤
│Cersei │0.022287327589773507│
├────────┼────────────────────┤
│Arya │0.022050209663844467│
└────────┴────────────────────┘
Community detection#
Community detection algorithms are used to find clusters in the graph. We'll use the walktrap method as implemented in igraph to find communities of characters that frequently interact within the community, but not much interaction occurs outside of the community.
We'll run the walktrap community detection algorithm and then write the newly discovered community numbers back to Neo4j, with the community each Character belongs to represented by an integer:
clusters = IGraph.community_walktrap(ig, weights="weight").as_clustering()
nodes = [{"name": node["name"]} for node in ig.vs]
for node in nodes:
idx = ig.vs.find(name=node["name"]).index
node["community"] = clusters.membership[idx]
write_clusters_query = '''
UNWIND {nodes} AS n
MATCH (c:Character) WHERE c.name = n.name
SET c.community = toInt(n.community)
'''
graph.run(write_clusters_query, nodes=nodes)
We can then query Neo4j to see how many communities (or clusters) we ended up with and the members of each community:
MATCH (c:Character)
WITH c.community AS cluster, collect(c.name) AS members
RETURN cluster, members ORDER BY cluster ASC
╒═══════╤═══════════════════════════════════════════════════════════════════════════╕
│cluster│members │
╞═══════╪═══════════════════════════════════════════════════════════════════════════╡
│0 │[Aemon, Alliser, Craster, Eddison, Gilly, Janos, Jon, Mance, Rattleshirt, S│
│ │amwell, Val, Ygritte, Grenn, Karl, Bowen, Dalla, Orell, Qhorin, Styr] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│1 │[Aerys, Amory, Balon, Brienne, Bronn, Cersei, Gregor, Jaime, Joffrey, Jon A│
│ │rryn, Kevan, Loras, Lysa, Meryn, Myrcella, Oberyn, Podrick, Renly, Robert, │
│ │Robert Arryn, Sansa, Shae, Tommen, Tyrion, Tywin, Varys, Walton, Petyr, Eli│
│ │a, Ilyn, Pycelle, Qyburn, Margaery, Olenna, Marillion, Ellaria, Mace, Chata│
│ │ya, Doran] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│2 │[Arya, Beric, Eddard, Gendry, Sandor, Anguy, Thoros] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│3 │[Brynden, Catelyn, Edmure, Hoster, Lothar, Rickard, Robb, Roose, Walder, Je│
│ │yne, Roslin, Ramsay] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│4 │[Bran, Hodor, Jojen, Luwin, Meera, Rickon, Nan, Theon] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│5 │[Belwas, Daario, Daenerys, Irri, Jorah, Missandei, Rhaegar, Viserys, Barris│
│ │tan, Illyrio, Drogo, Aegon, Kraznys, Rakharo, Worm] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│6 │[Davos, Melisandre, Shireen, Stannis, Cressen, Salladhor] │
├───────┼───────────────────────────────────────────────────────────────────────────┤
│7 │[Lancel] │
└───────┴───────────────────────────────────────────────────────────────────────────┘
Visualization - putting it all together#
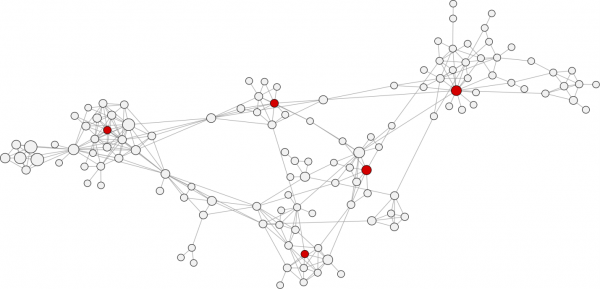
The graph of thrones. Node size is proportional to betweenness centrality, colors indicate the cluster of the node as determined by the walktrap method, and the edge thickness is proprtional to the number of interactions between two characters.
Now that we've computed these analytics for the graph, let's create a visualization that allows us to make sense of the data.
The Neo4j Browser is great for visualizing the results of Cypher queries, but if we want to embed our graph visualizations in another application we might want to use one of the many great Javascript libraries for graph visualizations. Vis.js is one such library that allows for building interactive graph visualizations. To make the process of pulling data from Neo4j and building graph visualizations with vis.js I've been working on neovis.js, which combines vis.js and the Neo4j official Javascript driver. Neovis.js provides a simple API that allows for configuring the visualization. For example, the following Javascript is all that is necessary to produce the visualization above:
var config = {
container_id: "viz",
server_url: "localhost",
labels: {
"Character": "name"
},
label_size: {
"Character": "betweenness"
},
relationships: {
"INTERACTS": null
},
relationship_thickness: {
"INTERACTS": "weight"
},
cluster_labels: {
"Character": "community"
}
};
var viz = new NeoVis(config);
viz.render();
Note that we have specified:
- We want to include nodes with the label
Characterin the visualization, using the propertynameas their caption - Node size should be proportional to the value of their
betweennessproperty - We want to include
INTERACTSrelationships in the visualization - The thickness of the relationships should be proportional to the value of the
weightproperty - The nodes should be colored according to the value of the propety
communitywhich identifies the clusters in the network - To pull the data from a Neo4j server on
localhost - To display the visualization in a DOM element with the id
viz
Neovis.js takes care of pulling the data from Neo4j and creating the visualization based on our minimal configuration.
Resources#
- A. Beveridge and J. Shan, "Network of Thrones" Math Horizons Magazine , Vol. 23, No. 4 (2016), pp. 18-22.
- J. Kleinberg and D. Easley, Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge University Press (2010)
All code is available on Github.
Subscribe To Will's Newsletter
Want to know when the next blog post or video is published? Subscribe now!